■ 06年10月29日(日)
コーラム論…6/交差とすれ違い
コーラムの描画規則をふまえた上で、そのバリエーションの生成システムについて考えてみたい。
まず最初に考えたのは、コーラムのパターンを何らかの記号や数値に置き換えることができないか、ということだ。前に示したように、コーラムの描線が通る道筋は下図のようにかなり限られている(この緑の点線を、描線の通りうる経路という意味で、仮に「仮定経路」と呼ぶことにする)。
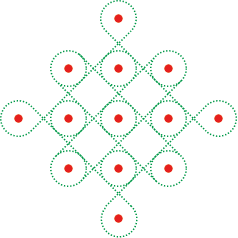
そこで、この図をじっくり眺めていると、コーラムの様々なパターンというのは、この仮定経路の交点(斜行格子の交点)部分の形状が、「交差(2直線の直交)」となるか「すれ違い(背反する2円弧)」になるか、の組み合わせでできていることに気付いたのである。
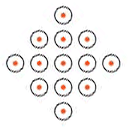
例えば仮定経路の各交点の形状を下図のように、●を「交差」、○を「すれ違い」として設定してみると、
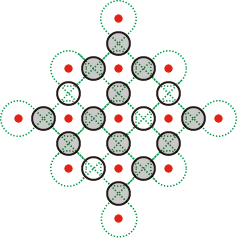
このようなパターンになるというわけだ。
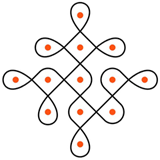
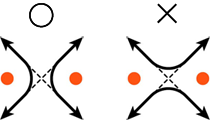
ちなみに全てを「交差」にすると左図、すべてを「すれ違い」にすると右図のようになる。
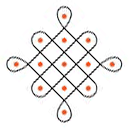
※すれ違いの方向は可能性としては2種類ありえるのだが、前述の描画規則(2)によって必ず点を中心とするように定められていることに注意。
ある配列点が与えられた時、仮定経路は自動的に定まる。
交点の位置と数も同時に定まる
交点の形状は2つに1つである。
ということは、仮定経路の各交点に「交差=1」と「すれ違い=0」という具合に値を割り当てやれば、すべてのコーラムのパターンを二進数の数値で表現できるということである。
数値化できるということの有効性は、例えばコンピューターを用いた網羅的な分析が可能になるということであり、例えばナンバリングによるコーラム紋様のデータベースなんてものがつくれるということだ。これは我ながら重大な発見であったと思う
次回は、数値化の具体的プロセスについて。
| 柳沢究, インド | PermaLink | trackbacks (0) |
トラックバック
■ Trackback-URL
http://www.kaguraoka.info/cgi/mt/mt-tb.cgi/131